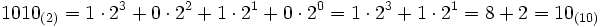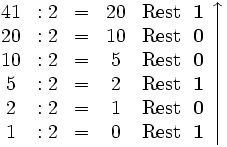Zahlensysteme

10 Ziffern: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Stellenwerttabelle:

Das Dualsystem (lat. dualis = zwei enthaltend), auch Binärsystem oder Zweiersystem genannt, ist ein Zahlensystem das nur zwei verschiedene Ziffern zur Darstellung von Zahlen benutzt.

Im gewöhnlich verwendeten Dezimalsystem werden die Ziffern 0 bis 9 verwendet. Im Dualsystem hingegen werden Zahlen nur mit Ziffern, welche die Werte Null oder Eins annehmen, dargestellt. Oft werden für diese Ziffern die Symbole 0 und 1 verwendet. Es ist auf Grund seiner Bedeutung in der Digitaltechnik nach dem Dezimalsystem das wichtigste Zahlensystem. Die Zahlen, die durch das Dualsystem dargestellt werden, heißen Dualzahlen oder Binärzahlen. Letztere ist die allgemeinere Bezeichnung, da diese auch einfach für binärcodierte Zahlen stehen kann. Der Begriff Binärzahl spezifiziert die Darstellungsweise einer Zahl also nicht näher, er sagt nur aus, dass zwei verschiedene Ziffern verwendet werden.

In älterer Literatur mit Bezug zur elektronischen Datenverarbeitung werden manchmal die Symbole Low (L) und High (H) anstelle von 0 und 1 verwendet. Low steht dann meist für den Wert Null und High für den Wert Eins. Diese Zuordnung nennt sich positive Logik, bei negativer Logik werden die Werte andersherum zugeordnet. Auch die Symbole L für den Wert Eins und 0 für den Wert Null finden Verwendung.

Null:  0
Eins:  1
Zwei:  10
Drei:  11
Vier:  100
Fünf:  101
Sechs:  110
Sieben:  111
Acht:  1000
Neun:  1001
Zehn:  1010

Um eine Dualzahl in die entsprechende Dezimalzahl umzurechnen, werden alle Ziffern jeweils mit ihrem Stellenwert (entsprechende Zweierpotenz) multipliziert und dann addiert. Beispiel:

Es gibt mehrere Möglichkeiten der Umrechnung ins Dualsystem. Im Folgenden ist die Divisionsmethode (auch Modulo-Methode genannt) am Beispiel 41 beschrieben:

Die entsprechende Dualzahl ergibt sich durch Notation der errechneten Reste von unten nach oben: 101001.

m Hexadezimalsystem (griech. hexa „sechs“ und lat. decem „zehn“, besser Sedezimalsystem von lat. sedecim „sechzehn“, auch als hexdekadisch bezeichnet) werden Zahlen in einem Stellenwertsystem mit der Basis 16 (also einem 16er-System) dargestellt.

n der Datenverarbeitung wird das Hexadezimalsystem neben dem Oktalsystem oft verwendet, um die Datenworte bei Computern, die oft aus Oktetten bestehen, in einer zweistelligen Hexadezimalzahl darzustellen. Im Gegensatz zum Dezimalsystem eignen sich das Hexadezimalsystem mit seiner Basis als vierte Zweierpotenz (16 = 24) sowie das Oktalsystem mit seiner Basis als dritte Zweierpotenz (8 = 23) nämlich gut zur Notation, da stets eine feste Anzahl Zeichen benötigt wird (zur Darstellung eines Oktetts mit 8 binären Ziffern werden nur zwei Hexadezimalziffern benötigt).

Das Hexadezimalsystem eignet sich sehr gut, um Folgen von Bits (verwendet in der Digitaltechnik) darzustellen. Vier Stellen einer Bitfolge (ein Nibble, auch Tetrade) werden wie eine Dualzahl interpretiert und entsprechen so einer Ziffer des Hexadezimalsystems, da 16 die vierte Potenz von 2 ist. Die Hexadezimaldarstellung der Bitfolgen ist leichter zu lesen und schneller zu schreiben.

Eine Möglichkeit, eine Zahl des Dezimalsystems in eine Zahl des Hexadezimalsystems umzurechnen, ist die Betrachtung der Divisionsreste, die entstehen, wenn die Zahl durch die Basis 16 geteilt wird. Im Beispiel der 1278 sähe das so aus:

1278 : 16 = 79 Rest: 14 (= E) (Nr:1278-(79*16)=14)

79 : 16 = 4 Rest: 15 (= F) (Nr:79-(4*16)=15)

4 : 16 = 0 Rest: 4 (Nr:4-(0*16)=4)

Die Hexadezimalzahl wird von unten nach oben gelesen und ergibt somit 4.F.E.