Gliederung

Liste 1

Liste 2

Klammern

Bruch

Gleichung 1

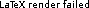
Gleichung 2

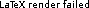
Wurzel

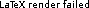
n-te Wurzel

Integral

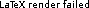
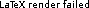
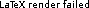
• peer:/usr/local/texlive/2007
• Einführung in das Textsatzsystem LaTeX

\documentclass[a4paper,10pt]{article}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage{ngerman} %für Texte in deutscher Sprache nach neuer Rechtschreibung
\usepackage[T1]{fontenc} %ermöglicht zusätzlich die Silbentrennung bei Wörtern, die Umlaute enthalten
\usepackage[utf8]{inputenc} %ermöglicht die Eingabe der Umlaute und ß direkt über die Tastatur

%opening
\title{Wiederholungsprüfung}
\author{Peer}

\begin{document}
\begin{enumerate}
 \item 
 \item
\end{enumerate}
\end{document}

\documentclass[11pt,fleqn]{scrartcl}
\usepackage{ucs}
\usepackage[utf8x]{inputenc}
\usepackage{ngerman}
\usepackage{graphicx}
\usepackage{amsmath,amssymb,amstext,bbm}
\usepackage[automark]{scrpage2}
\title{Formelheft}
\author{Helmuth Peer}
\date{\today{}, Weiz}
\begin{document}
\maketitle
\thispagestyle{empty}% weil \maketitle ggf. ein \thispagestyle{plain} enthält 
\tableofcontents
%\pagestyle{empty}
%\ifoot[]{Peer}
%\cfoot{}
%\ofoot{}

%Tabellenzwischenräume vergrößern/verändern
%Spaltenzwischenraum zwischen zwei benachbarten Spalten  
\setlength{\tabcolsep}{10pt}
%Zeilenabstand innerhalb der Tabelle
\renewcommand{\arraystretch}{2}

\newpage
\section{Potenzen}
$a, b \in \mathbb{R}, r, s \in \mathbb{R}, k \in \mathbb{Z}, m, n \in
\mathbb{N}^{\ast}$\\
%\vspace{5cm}\\
\begin{tabular}{|c|c|c|c|c|}
\hline
$a^0 = 1$ & $a^1 = a$ & $a^{- n} = \frac{1}{a^n} = \left( \frac{1}{a} \right)^n$ & $a^{\frac{1}{n}} = \sqrt[n]{a}$&

$a^{\frac{k}{n}} = \sqrt[n]{a^k}$ \\

\hline

\end{tabular}\\
\begin{tabular}{|c|c|}
\hline
$a^r \cdot a^s = a^{r + s}$ & $\sqrt[n]{a^k} = \sqrt[n \cdot m]{a^{k \cdot m}}$\\\hline
$a^r : a^s = a^{r - s}$ & $\sqrt[n]{\sqrt[m]a} = \sqrt[n \cdot m]{a}$\\\hline
$(a^r)^s=a^{r \cdot s}$ & $( \sqrt[n]{a})^k = \sqrt[n]{a^k}$\\\hline
$(a \cdot b)^r = a^r \cdot b^r$ & $\sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}$\\\hline
$( \frac{a}{b})^r= \frac{a^r}{b^r}$ & $\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}$\\\hline
\end{tabular}



  
$(a \pm b)^2 = a^2 \pm 2 ab + b^2$


\section{Logarithmen}

\(^{10}\)log a = 1\\
$a, b \in \mathbbm{R}^+ \backslash \left\{ 1 \right\},
u, v \in \mathbbm{R}^+, r \in \mathbbm{R}, n \in \mathbbm{N}^{\ast} \bot \in
\backslash$

\[e = \lim_{n \rightarrow \infty} \left( 1 + \frac{1}{n} \right)^n\]

\[ \lim_{n \rightarrow \infty} \left( 1 + \frac{1}{n} \right)^n = 2, 71828 \dots \]

\section{Quadratische Gleichungen}

\[x^2 + px + q = 0\]

\[x = - \frac{p}{2} \pm \sqrt{\left( \frac{p}{2} \right)^2 - q}\]

\begin{tabular}{|c|c|}
  \hline
  $x^2 + px + q = 0$ & $ax^2 + bx + c = 0$\\
  \hline
  $x = - \frac{p}{2} \pm \sqrt{\left( \frac{p}{2} \right)^2 - q}$ & $x = \frac{- b \pm \sqrt{b^2 - 4 ac}}{2 a}$\\
 \hline
\end{tabular}

\section{Komplexe Zahlen}

\(z = a + bi \in \mathbbm{C} \Leftrightarrow a, b \in \mathbbm{R}
\ \mbox{und} \ i^2 = - 1 ; \sqrt{- a} = i \sqrt{a} \ \mbox{mit} \ a > 0\) \\
$(a + bi) (a - bi) = a^2 + b^2$

$\left| z \right| = r = \sqrt{a^2 + b^2}$

$\arg z = \varphi \in [0^{\circ} ; 360^{\circ} [$

%\includegraphics{oelta002.png}

\section{Schaltalgebra}



$a \vee b = b \vee a$

$a \wedge b = b \wedge a$
\section{Vektoren}

\subsection{Vektorielles Produkt}

$\vec{a} = \left(\begin{array}{c}
  a_1\\
  a_2\\
  a_3
\end{array}\right) \times \left(\begin{array}{c}
  b_1\\
  b_2\\
  b_3
\end{array}\right) = \left(\begin{array}{c}
  \left|\begin{array}{c}
    a_2 b_2\\
    a_3 b_3
  \end{array}\right|\\
  - \left|\begin{array}{c}
    a_1 b_1\\
    a_3 b_3
  \end{array}\right|\\
  \left|\begin{array}{c}
    a_1 b_1\\
    a_2 b_2
  \end{array}\right|
\end{array}\right) = \left(\begin{array}{c}
  a_2 b_3 - a_3 b_2\\
  a_3 b_1 - a_1 b_3\\
  a_1 b_2 - a_2 b_1
\end{array}\right)$

\section{Analytische Geometrie}

$\overrightarrow{\text{AB}} = B - A$

\subsection{Flächeninhalt Parallelogramm}

$A_p = \sqrt{\vec{a}^2 \cdot \vec{b}^2 - ( \vec{a} \cdot \vec{b})^2}$



\subsection{Parameterdarstellung einer Geraden}

$\vec{x} = \left(\begin{array}{c}
  1\\
  2\\
  3
\end{array}\right) + t \cdot \left(\begin{array}{c}
  4\\
  5\\
  6
\end{array}\right)$

\section{Differential- und Integralrechnung}

\subsection{Ableitungs- und Stammfunktionen}

\begin{tabular}{|l|l|l|}
  \hline
  Funktion & Ableitungsfunktion & Stammfunktionen\\
  \hline
  $y = f (x) = k$ & $y' = f' (x) = 0$ & $F (x) = \int \mbox{kdx} = \mbox{kx} + C$\\\hline
  $y = f (x) = x^q$ & $y' = f' (x) = q \cdot x^{q - 1}$ & $q \neq - 1 :$ \\\hline
  &  & $F (x) = \int x^q \mbox{dx} = \frac{x^{q + 1}}{q + 1} + C$\\\hline
\end{tabular}

\subsection{Rauminhalte}

\subsubsection{Drehk\"orper}

Drehung um die x-Achse:

\(V = \pi \int^b_a y^2 \mbox{dx}\)

\subsection{Numerische Integration}

\subsubsection{Rechtecksformel}

$\int^b_a f (x) \mbox{dx} \approx \frac{b - a}{n} \cdot [f (x_0) + f (x_1) + f
(x_2) + \ldots . + f (x_{n - 1})] = \Delta x \cdot \sum^{n - 1}_{i = 0} f
(x_i)$
\[ \Delta x \cdot \sum_{i = 0}^{i - 1} f (x_i) \]

\subsection{Binomialverteilung}

$P (X = k) = b_{n, p} (k) = \left(\begin{array}{c}
  n\\
  k
\end{array}\right) p^k (1 - p)^{n - k}$

\subsection{Normalverteilung}

$\varphi (x) = \frac{1}{\sqrt{2 \pi}} e^{- \frac{x^2}{2}}$


\[ \Phi (z) = \int^z_{- \infty} \varphi (x) \text{dx} = \frac{1}{\sqrt{2 \pi}}
   \int^z_{- \infty} e^{- \frac{x^2}{2}} \mbox{dx} \]




\end{document}